神奇的整数划分 DP

一个不会整数划分的 sb 的自救

考虑一个这样的问题：给定 $n,m$ ，求将 $m$ 划分成不超过 $n$ 个从 $1$ 开始值域连续的整数的和的方案数。

有一个很明显的做法：设 $f_{i,j,k}$ 表示用了 $i$ 个数，总和为 $j$ ，目前最大数为 $k$ 的方案数。转移比较明显：

$\begin{aligned} f_{i,j,k}&\rightarrow f_{i+1,j+k,k}\\ f_{i,j,k}&\rightarrow f_{i+1,j+k+1,k+1} \end{aligned}$

由于第三维最大到 $\sqrt{m}$ ，所以复杂度为 $\mathcal{O}(nm\sqrt{m})$ 。遗憾的是，原题 $n,m\leq 10^5$ 。

转移是无法优化了，我们只能从状态入手优化 $\rm{DP}$ 。我们假设最后的方案是 $\{1,2,2,3,4\}$ 。画出来看看：

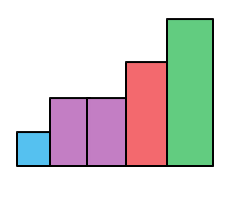
我们把这张图旋转 $90^{\circ}$：

可以发现，在第二张图中，我们将原来的限制：

• 不超过 $n$ 个数
• 值域连续
• 单调不降

转化成了

• 最大数不超过 $n$
• 每个数至多使用 $1$ 次
• 单调递减

事实上，我们每求出一个方案，就把它排序，这样第三个限制形同虚设。我们只需要考虑前两个限制。

先不考虑最大数的限制。设 $f_{i,j}$ 表示放了 $i$ 个数，总和为 $j$ 的方案数。每次我们有两种转移：整体加一；整体加一，然后在末尾添 $1$ 。这个转移方式很经典，它保证了每个数至多使用一次。

考虑这种转移方式为什么不会算重。在最终的状态中，不会有相同的数；如果当前最小值是 $1$ ，我们就把 $1$ 去掉，并整体减一；否则直接整体减一。这样递归撤回到 $f_{0,0}$ 的方案是唯一的，所以从 $f_{0,0}$ 转移到这个状态的方案也是唯一的。

现在加上最大数的限制。可以发现，当不满足最大数的限制时，一定是当前最大数恰好为 $n+1$，并且只有它一个 。我们钦定最大数，直接减去这种方案的方案数即可。

转移方程如下，复杂度 $\mathcal{O}(m\sqrt{m})$：

$f_{i,j}\leftarrow f_{i-1,j-i} +f_{i,j-i}-f_{i-1,j-(n+1)}$

总的来说，这个题目的模型转化，和最后对最大数的容斥都是很妙的。希望自己多少能学到点。

还看到过一个有趣的整数划分题：求将 $n$ 划分成若干个奇正整数的方案数。

设 $o_{i,j}$ 表示将 $i$ 划分成 $j$ 个奇正整数的方案数，$e_{i,j}$ 表示将 $i$ 划分成 $j$ 个偶正整数的方案数。那么有以下两种转移：

• 对于偶数划分，把它们全部减一，就成了奇数划分。
• 对于奇数划分，按照是否有一分成两类。如果没有一，那么可以全部减一转化为偶数划分。

也就是说：

$\begin{aligned} e_{i,j}&\leftarrow o_{i-j,j}\\ o_{i,j}&\leftarrow o_{i-1,j-1}+e_{i-j,j} \end{aligned}$