Parallelist

浅い夢だから 胸をはなれない

HNOI2015 解题报告

发布于 2021-01-12 | 分类于 比赛报告 | 24分钟 | 4764字数 | 浏览量：

T1 菜肴制作

Description

有 nn 道菜和有 mm 条要求，每条要求形如“A 号菜需要在 B 号菜的前面”。现在要求给出一个上菜序列，在满足所有要求的前提下，满足：

  • 1 号菜肴尽量优先
  • 1 号菜肴尽量优先的情况下，2 号菜肴尽量优先
  • ...

n,m≤105n,m\leq 10^5

Solution

注意到这个题对于两个排列的比较方式不是字典序，而是“在 1∼i1\sim i 的位置相同时，满足 i+1i+1 的位置最小”这样的比较方式。

对于字典序的比较，我们采取的通法是值小的尽量靠前；
而对于本题的比较，我们采取的通法是值大的尽量靠后。

证明可以从比较方式入手考虑。假设当前有若干个值可以放在目前最后的位置，最后比较时，一定会先看那些值小的；如果不把目前最大值放在最后，那么我们可以视作最大值与某个值交换了，对其余的数字无影响。也就是说，如果把值小的放在目前最后的位置，一定是不优的。

知道了 trick 那么这个题目就很明显了。拓扑排序贪心选择即可。复杂度 O(nlog⁡2n)\mathcal{O}(n\log_2{n}) 。

Code

const int N=1e5+6;
using namespace std;
int n,m,top,d[N],ans[N];
vector<int>g[N];
priority_queue<int>q;
void solve(){
    r(n,m);top=0;
    for(int i=1;i<=n;++i) g[i].clear(),d[i]=0;
    for(int i=1,x,y;i<=m;++i)
        r(x,y),g[y].push_back(x),++d[x];
    for(int i=1;i<=n;++i)
        if(!d[i]) q.push(i);
    while(!q.empty()){
        int u=q.top();ans[++top]=u;q.pop();
        for(auto v:g[u])
            if((--d[v])==0) q.push(v); 
    }
    if(top<n) return puts("Impossible!"),void();
    while(top)
        w(ans[top--],' ');puts("");
}

T2 接水果

Description

给定一棵 nn 个点的树，pp 个 A 类路径和 qq 个 B 类路径。A 类路径有三个属性，为起始节点 ss 终止节点 tt 权值 w ；B 类路径有三个属性，为起始节点 ss 终止节点 tt 以及参数 kk 。对于每条 B 类路径，保证有不少于 kk 条 A 类路径是其子路径，求这些是其子路径的 A 类路径的权值第 kk 小。
1≤n,p,q≤4×1041\leq n,p,q\leq 4\times 10^4

Solution

要求对每条 B 类路径求权值第 kk 小，考虑整体二分。
二分权值 vv ，每次只管权值不大于 vv 的 A 类路径。问题转化为如何求每个 B 包含的 A 的数量。也就是如何快速判定一条路径是不是其余路径的子路径。
小 trick ：判定路径是否是子路径可以通过矩形覆盖来实现。

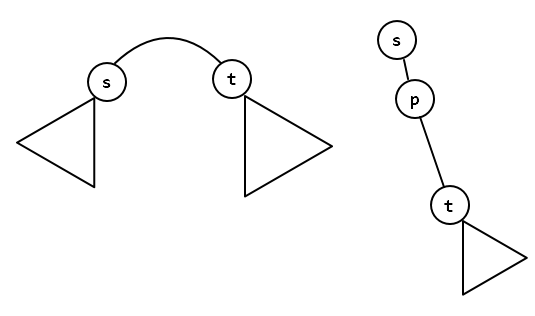
如左图，满足路径 s→ts\rightarrow t 是其子路径的路径端点必然一个在 ss 子树内，一个在 tt 子树内。如果记下来进/出每个点的子树时的 dfn 序，那么视作一个二维平面上的矩形。
如右图，满足路径 s→ts\rightarrow t 是其子路径的路径端点必然一个在 pp 子树的补集内，一个在 tt 子树内。可以视作两个矩形。
上面两种情况分开处理就好啦。
复杂度 O(nlog⁡22n)\mathcal{O}(n\log^2_2{n}) 。

Code

const int N=4e4+5;
using namespace std;
int n,p,q,tot,num,cnt;
int head[N],nt[N<<1],to[N<<1];
int o[N],lg[N],inp[N],out[N],ans[N],dep[N],f[N][20];
struct Query{
   int x,y,z,id;
   Query(int x=0,int y=0,int z=0,int id=0):
       x(x),y(y),z(z),id(id) {}
   bool operator <(const Query &b)const{
       return x<b.x;
   }
}Q[N],Qt[N];
struct Line{
   int x,t,b,v,val;
   Line(int x=0,int b=0,int t=0,int v=0,int val=0):
       x(x),b(b),t(t),v(v),val(val) {}
   bool operator <(const Line &b)const{
       return x<b.x;
   }
}A[N<<2],At[N<<2];
namespace BIT{
#define lowb(x) (x&(-x))
   int t[N];
   void add(int p,int v){
       while(p<=n)
           t[p]+=v,p+=lowb(p);
   }
   int query(int p){
       int ret=0;
       while(p) ret+=t[p],p-=lowb(p);
       return ret;
   }
   void modify(int b,int t,int v){
       add(b,v);add(t+1,-v);
   }
}
using BIT::modify;
using BIT::query;
void solve(int AL,int AR,int QL,int QR,int VL,int VR){
   if(AL>AR||QL>QR) return;
   if(VL==VR){
       for(int i=QL;i<=QR;++i)
           ans[Q[i].id]=o[VL];
       return;
   }
   int mid=VL+VR>>1;
   int now=AL,Atl=AL,Atr=AR,Qtl=QL,Qtr=QR;
   for(int i=QL;i<=QR;++i){
       while(now<=AR&&A[now].x<=Q[i].x) {
           if(A[now].val>o[mid]) At[Atr--]=A[now];
           else modify(A[now].b,A[now].t,A[now].v),At[Atl++]=A[now];
           ++now;
       }
       int v=query(Q[i].y);
       if(v>=Q[i].z) Qt[Qtl++]=Q[i];
       else Q[i].z-=v,Qt[Qtr--]=Q[i]; 
   }
   while(now<=AR) {
       if(A[now].val>o[mid]) At[Atr--]=A[now];
       else modify(A[now].b,A[now].t,A[now].v),At[Atl++]=A[now];
       ++now;
   }
   
   for(int i=AL;i<Atl;++i) modify(At[i].b,At[i].t,-At[i].v);
   for(int i=AL;i<Atl;++i) A[i]=At[i];for(int i=AR;i>Atr;--i) A[i]=At[i];
   for(int i=QL;i<Qtl;++i) Q[i]=Qt[i];for(int i=QR;i>Qtr;--i) Q[i]=Qt[i];
   reverse(A+Atr+1,A+AR+1);reverse(Q+Qtr+1,Q+QR+1);
   solve(AL,Atl-1,QL,Qtl-1,VL,mid);solve(Atr+1,AR,Qtr+1,QR,mid+1,VR);
}
void dfs(int p,int fa){
   inp[p]=++cnt;f[p][0]=fa;dep[p]=dep[fa]+1;
   for(int i=0;f[p][i];++i) f[p][i+1]=f[f[p][i]][i];
   for(int i=head[p];i;i=nt[i])
       if(to[i]^fa) dfs(to[i],p);
   out[p]=cnt;
}
int jump(int p,int h){
   while(h){
       int now=f[p][lg[h]-1];
       h-=dep[p]-dep[now];
       p=now;
   }
   return p;
}
void Add(int x,int y){
   ++num;nt[num]=head[x];head[x]=num;to[num]=y;
   ++num;nt[num]=head[y];head[y]=num;to[num]=x;
}
int main(){

   r(n,p,q);
   for(int i=1,a,b;i<n;++i)
       r(a,b),Add(a,b);
   dfs(1,0);
   for(int i=1;i<=n;++i)
       lg[i]=lg[i-1]+(1<<lg[i-1]==i);
   for(int i=1,a,b,c;i<=p;++i){
       r(a,b,c);o[i]=c;
       if(inp[a]>inp[b]) swap(a,b);
       if(out[a]>=out[b]){                // b in a
           int v=jump(b,dep[b]-dep[a]-1);
           A[++tot]=Line(1,inp[b],out[b],1,c);
           A[++tot]=Line(inp[v],inp[b],out[b],-1,c);
           if(out[v]<n){
               A[++tot]=Line(inp[b],out[v]+1,n,1,c);
               A[++tot]=Line(out[b]+1,out[v]+1,n,-1,c);
           }
       }   
       else{
           A[++tot]=Line(inp[a],inp[b],out[b],1,c);
           A[++tot]=Line(out[a]+1,inp[b],out[b],-1,c);
       }
   }
   for(int i=1,x,y,k;i<=q;++i){
       r(x,y,k);
       if(inp[x]>inp[y])
           swap(x,y);
       Q[i]=Query(inp[x],inp[y],k,i);
   }
   sort(Q+1,Q+q+1);
   sort(o+1,o+p+1);
   sort(A+1,A+tot+1);
   solve(1,tot,1,q,1,p);
   for(int i=1;i<=q;++i)
       w(ans[i]);
   return 0;
}

T3 实验比较

Description

给一个 nn 个点的外向树森林。要求给 nn 个点赋权值，满足

  • 权值必须连续。
  • 父节点的权值小于子节点的权值。
  • 可以给不同的点赋相同权值。

赋完权值后给所有点排序，权值相等的点按照编号排序，然后用 '<' 或者 '=' 连接相邻两个数。求有多少种不同的最后的序列（符号不同也可以）。

1≤n≤1001\leq n\leq 100

Solution

我们考虑最终的序列中 ，kk 个小于号将序列分成了 k+1k+1 段。
于是转化为了经典的按照段来划分的子树合并。
设原来的序列为 A ，目前合并的序列为 B ，新的序列为 C 。C 有如下三个限制：

  • C 的第一段必然是当前节点本身，同时也是 A 的第一段。
  • C 的任意一段非空。
  • C 除第一段以外的任意一段要么由 B 组成，要么由 A 组成，要么由 A B 共同组成。

枚举 C 的前 ii 段，枚举 A 的 jj 段，枚举 B 的 kk 段来合并。

f[p][i]=f[u][k]×f[p][j]×(i−1j−1)(j−1j−(k−i))f[p][i]=f[u][k]\times f[p][j]\times \binom{i-1}{j-1}\binom{j-1}{j-(k-i)}

第一个组合数的意义是如何放 A 的 jj 段，第二个组合数的意义是如何合并。
复杂度 O(n3)\mathcal{O}(n^3)

Code

void dp(int p,int fa=0){
    sz[p]=f[p][1]=1;
    for(int i=head[p];i;i=nt[i])if(to[i]^fa){
        int u=to[i];dp(u,p);
        memset(tmp,0,sizeof tmp);
        for(int k=1;k<=sz[p]+sz[u];++k)
        for(int i=1;i<=sz[p];++i)
        for(int j=1;j<=sz[u];++j){
            int x=j-(k-i);if(x<0) continue;
            tmp[k]=Plus(1ll*tmp[k],1ll*f[p][i]*f[u][j]%mod*c[k-1][i-1]%mod*c[i-1][x]%mod);
        }
        sz[p]+=sz[u];
        for(int k=1;k<=sz[p];++k)
            f[p][k]=tmp[k];
    }
}

T4 亚瑟王

Description

有 nn 张卡牌，每张卡牌有两个属性：伤害值 did_i 和发出技能的概率值 pip_i 。在每一轮中，系统将从第一张卡牌开始，按照顺序枚举每张卡牌。如果当前的卡牌 ii 已经发动过技能，则直接跳过；否则，有 pip_i 的概率放出技能并结束这一轮，1−pi1-p_i 的概率未放出，并枚举下一张卡牌。
给定 nn 和游戏轮数 rr ，求期望造成的伤害。T 组数据。
1≤T≤444,1≤n≤220,1≤r≤132,0<pi<11\leq T \leq 444,1\leq n\leq 220,1\leq r\leq 132,0< p_i< 1

Solution

期望的题目一般都要分开计算贡献。如本题，若求出来了第 ii 张卡牌放出技能的概率 gig_i ，那么期望就好做了。
直接求放出技能的概率还需要枚举第几轮放出来的，我们转化成枚举补集，计算不放出的概率。
可以发现一个重要的性质：由于是顺序枚举，所以当 ii 之前的卡牌释放技能时，ii 本轮就不用经历 1−pi1-p_i 的抉择。也就是说，若 ii 之前有 kk 个卡牌释放了技能，那么 ii 不放出的概率是 (1−pi)r−k(1-p_i)^{r-k}
设 f[i][j] 表示在 rr 轮中，前 ii 张卡片释放出 jj 次技能的概率。考虑第 ii 张卡牌是否释放技能可得：

f[i][j]=f[i−1][j−1]×(1−(1−p[i])r−(j−1))f[i][j]=f[i−1][j]×(1−p[i])r−j\begin{aligned} f[i][j]&=f[i-1][j-1]\times (1-(1-p[i])^{r-(j-1)})\\ f[i][j]&=f[i-1][j]\times (1-p[i])^{r-j}\\ \end{aligned}

求出来 f 数组，求出 i 不放出的概率就好做了。
复杂度 O(Tn2)\mathcal{O}(Tn^2) 。

Code

void solve(){
    cin>>n>>m;
    memset(f,0,sizeof f);
    memset(q,0,sizeof q);
    for(int i=1;i<=n;++i)
        cin>>p[i]>>d[i];
    for(int i=1;i<=n;++i){
        q[i][0]=1,q[i][1]=1-p[i];
        for(int j=2;j<=m;++j) 
            q[i][j]=q[i][j-1]*(1-p[i]);
    }
    f[0][0]=1;
    for(int i=1;i<n;++i)
    for(int j=0;j<=i&&j<=m;++j){
        f[i][j]+=f[i-1][j]*q[i][m-j];
        if(j) f[i][j]+=f[i-1][j-1]*(1-q[i][m-j+1]);
    }
    double ans=0;
    for(int i=1;i<=n;++i){
        double tmp=0;
        for(int j=0;j<=i-1;++j)
            tmp+=f[i-1][j]*(1-q[i][m-j]);
        ans+=tmp*d[i];
    }
    printf("%.10lf\n",ans);
}

T5 落忆枫音

Description

给一张 nn 个点的 DAG 和一条边，求以 1 为根的外向树个数。保证 1 号点没有入边。
1≤n≤105,1≤m≤2×1051\leq n\leq 10^5,1\leq m\leq 2\times 10^5

Solution

设 d[i] 表示 ii 号点的入度。钦定 1 号点的入度为 1 。
若没有额外的边，我们考虑树上每个点的父亲可得外向树个数为

∏i=1ndi\prod_{i=1}^{n}d_i

现在有了额外的边，意味着任意连边的话可能连出环。我们需要减去不合法的方案。
假设这条边为 s→ts\rightarrow t 。s→ts\rightarrow t 这条边连上后可能会形成若干个环，这些环的方案之间相互独立（因为生成树内不可能同时有两个环），于是我们单独考虑某个环。
若这个环上的点为 a1,a2,⋯ ,aka_1,a_2,\cdots,a_k ，我们钦定环上的点在树上也恰好连成一个环，那么方案为：

∏i=1ndi∏i=1kdai\frac{\prod\limits_{i=1}^{n}d_i}{\prod\limits_{i=1}^{k}d_{a_i}}

于是统计每一个成环的方案就行了。这个我们可以从 t 出发找 s ，在 dfs 的时候顺便统计。
但是最多有 n 个环，暴力做是 O(n2)\mathcal{O}(n^2) 的。
在经过了某个点后，从该点出发到 s 的这些路径上的权值是不变的。我们可以设为 f[p] 。
那么有转移

f[p]=1dp∑f[u]f[p]=\frac{1}{d_p}\sum f[u]

边界条件为 fs=∏i=1ndidsf_s=\frac{\prod\limits_{i=1}^{n}d_i}{d_s} 。
最终的答案就是 ∏i=1ndi−ft\prod\limits_{i=1}^{n}d_i-f_t 。复杂度为 O(n)\mathcal{O}(n) 。

Code

int f[N],ans=1;
void dp(int p){
    if(vis[p]) return void();vis[p]=1;
    if(p==s){
        f[p]=1ll*ans*Q(ind[p],mod-2)%mod;
        return;
    }
    for(auto v:c[p]) dp(v),f[p]=(f[p]+f[v])%mod;
    f[p]=1ll*f[p]*Q(ind[p],mod-2)%mod;
}
int main(){

    r(n,m,s,t);c[s].push_back(t);
    for(int i=1,x,y;i<=m;++i)
        r(x,y),c[x].push_back(y),++ind[y];
    ++ind[1];++ind[t];
    for(int i=1;i<=n;++i)
        ans=1ll*ans*ind[i]%mod;
    dp(t);
    w((ans-f[t]+mod)%mod);
    return 0;
}

T6 开店

Description

给定一棵 nn 个点的树，每个点有一个妖怪，年龄为 xix_i 。qq 次询问，每次幽香打算在 uu 建立一个面向年龄 L 到 R 之间的便利店，她需要你告诉她所有年龄在 L 到 R 之间的妖怪，到点 uu 的距离的和是多少
n,q≤2×105n,q\leq 2\times 10^5 。

Solution

建点分树，每个点用 vector 维护自己的贡献和需容斥的值。
注意 O(nlog⁡2n)\mathcal{O}(n\log^2n) 的空间是无法通过本题的（也就是不能用线段树来维护）。
做题时不应该放弃用 vector 维护的可能。vector 上二分也是较好的选择。

Code

struct L{
    int cnt,tot;
    int fst[N],dep[N],dfn[N],idx[N],eul[N<<1],lg[N<<1],f[N<<1][20];
    void dfs(int p,int fa){
        dfn[p]=++cnt;idx[cnt]=p;
        eul[++tot]=cnt;fst[p]=tot;
        for(int i=head[p];i;i=nt[i])
            if(to[i]!=fa) dep[to[i]]=dep[p]+val[i],dfs(to[i],p),eul[++tot]=dfn[p];
    }
    void Init(){
        dfs(1,0);
        for(int i=1;i<=tot;++i) f[i][0]=eul[i];
        for(int i=2;i<=tot;++i) lg[i]=lg[i>>1]+1;
        for(int j=1;j<=lg[tot];++j)
        for(int i=1;i+(1<<j)-1<=tot;++i)
            f[i][j]=min(f[i][j-1],f[i+(1<<j-1)][j-1]);
    }
    inline int LCA(int x,int y){
        x=fst[x],y=fst[y];
        if(x>y) swap(x,y);
        int k=lg[y-x+1];
        return idx[min(f[x][k],f[y-(1<<k)+1][k])];
    }
    inline int dis(int x,int y){return dep[x]+dep[y]-dep[LCA(x,y)]*2;}
}l;
inline void Add(int x,int y,int z){
    ++num;nt[num]=head[x];head[x]=num;to[num]=y;val[num]=z;
    ++num;nt[num]=head[y];head[y]=num;to[num]=x;val[num]=z;
}
void Getrt(int p,int fa){
	int Max=0;size[p]=1;
	for(int i=head[p];i;i=nt[i]){
		if(to[i]==fa||lock[to[i]]) continue;
		Getrt(to[i],p);size[p]+=size[to[i]];
		Max=max(Max,size[to[i]]);
	}
	Max=max(Max,Part-size[p]);
	if(Max<Min) rt=p,Min=Max;
}
void solve(int p,int fa,int sz){
	par[p]=fa;lock[p]=1;dsz[p]=sz;
	int tmp=Part;
	for(int i=head[p];i;i=nt[i]){
		if(lock[to[i]]) continue;
		if(size[to[i]]>size[p]) Part=tmp-size[p];
		else Part=size[to[i]];
		Min=n+1;Getrt(to[i],p);solve(rt,p,Part);
	}
}
struct Node{
    long long v,d,c;
    Node(long long v=0,long long d=0,long long c=0):v(v),d(d),c(c) {}
    Node operator -(const Node &b)const{return Node(0,d-b.d,c-b.c);}
    bool operator <(const Node &b)const{return v<b.v;}
};
vector<Node>v[N<<1];
#define iter vector<Node>::iterator 
void Build(){
    for(int i=1;i<=n;++i){
        v[i].push_back(Node(X[i],0,1));
        v[i].push_back(Node(-1,0,1));v[i+n].push_back(Node(-1,0,1));
        for(int j=i;par[j];j=par[j]){
            int d=l.dis(i,par[j]);
            v[par[j]].push_back(Node(X[i],d,1));
            v[j+n].push_back(Node(X[i],d,1));
        }
    }
    for(int i=1;i<=n;++i){
        sort(v[i].begin(),v[i].end());
        sort(v[i+n].begin(),v[i+n].end());
        int sz=v[i].size();
        for(int j=1;j<sz;++j)
            v[i][j].d+=v[i][j-1].d,v[i][j].c+=v[i][j-1].c;
        sz=v[i+n].size();
        for(int j=1;j<sz;++j)
            v[i+n][j].d+=v[i+n][j-1].d,v[i+n][j].c+=v[i+n][j-1].c;
        
    }
}

inline Node Calc(int u,int L,int R){
    int sz=v[u].size();
    iter t1=upper_bound(v[u].begin(),v[u].end(),Node(L-1,0,0)),t2=upper_bound(v[u].begin(),v[u].end(),Node(R,0,0));
    --t1;--t2;
    return Node(*(t2)-*(t1));
}
long long Query(int u,int L,int R){
    long long ret=Calc(u,L,R).d;
    for(int i=u;par[i];i=par[i]){
        long long d=l.dis(u,par[i]);
        Node cur1=Calc(par[i],L,R),cur2=Calc(i+n,L,R);
        ret+=(cur1.d-cur2.d);
        ret+=1ll*(cur1.c-cur2.c)*d;
    }
    return ret;
}
int main(){

    r(n),r(q),r(A);
    for(int i=1;i<=n;++i) 
        r(X[i]),++X[i];
    for(int i=1,x,y,z;i<n;++i)
        r(x),r(y),r(z),Add(x,y,z);
    Min=n+1;Part=n;Getrt(1,0);solve(rt,0,n);
    long long las=0;l.Init();Build();
    for(int i=1,u,a,b;i<=q;++i){
        r(u),r(a),r(b);
        int L=min((a+las)%A+1,(b+las)%A+1),R=max((a+las)%A+1,(b+las)%A+1);
        w(las=Query(u,L,R));putchar(10);
    }
    return 0;
}

Analysis

HNOI2015 的质量挺高，整体码量不大，个别题目码量不小。有 3 道 动态规划 2 道数据结构 1 道贪心。应该算是一场比较标准的比赛。
菜肴制作 考察了一个可能比较常见的 trick 。所以说平常也要多打 Atcoder/Codeforces 的比赛来积累这些方法。
接水果 考察了整体二分和矩形覆盖。整体二分可以从题目描述中想到，矩阵覆盖需要手玩“路径的子路径”的性质来发现。dfs 序是很活的东西，平常也要多想，做题时也要额外思考一下。
实验比较 考察了树上合并和排列组合。这类题目思路差不多，在实际做的时候想清楚状态推好式子。
亚瑟王 考察了概率期望。做题目时不应总是想着用线性性解决一切，有时也可以从条件概率的角度出发，找到条件的特点，转化问题。
落忆枫音 考察了计数 dp 。如果可以想到枚举生成树上每个点的父亲题目就好做了。
开店 考察了点分树。合理选择点分树内部进行计算/容斥的数据结构是点分树的精华所在。

# 比赛报告
SPOJ3734 Periodni 上一篇
CF932G Palindrome Partition 下一篇
0%