Parallelist

浅い夢だから 胸をはなれない

拟阵及拟阵交

发布于 2021-01-17 | 分类于 拟阵 、 学习笔记 | 15分钟 | 3161字数 | 浏览量：

定义

定义 EE 为基础集，I\mathcal{I} 是由 EE 的子集构成的集族（子集的集合）。
元组 (E,I)(E,\mathcal{I}) 构成了一个子集系统，当且仅当

  • EE 是一个有限集。
  • I\mathcal{I} 是有限非空集。
  • ∀B∈I\forall B\in\mathcal{I}，∀A⊂B\forall A\subset B，有 A∈IA\in\mathcal{I}（可知 ∅∈I\emptyset\in \mathcal{I} ） 。这条性质称为遗传特性。

我们称子集系统 M=(E,I)\mathcal{M}=(E,\mathcal{I}) 是拟阵，它还需要满足下面的性质。

  • ∀∣A∣<∣B∣\forall |A|<|B|，若 A∈IA\in \mathcal{I} 且 B∈IB\in \mathcal{I}，则 ∃x∈B−A\exist x\in B-A，A∪{x}∈IA\cup \{x\}\in \mathcal{I} 。这条性质称为交换特性。

在拟阵中，I\mathcal{I} 中的元素称为独立集。

拟阵是一个抽象的概念。满足了这四个性质的 (E,I)(E,\mathcal{I}) 均可以称作拟阵。
实际情况中，拟阵的构造难点一般在遗传特性和交换特性。

对于 U⊆EU\subseteq E ，我们定义 UU 的秩为 r(U)=max⁡{∣x∣∣x⊆U,x⊆I}r(U)=\max\{|x||x\subseteq U,x\subseteq \mathcal{I}\} 。

简单实例

背包问题

假设我们只能用 Max\text{Max} 个体积。先进行转化：将体积为 vv ，单位价值为 ww 的物品变成 vv 个体积为 11 ，价值为 ww 的物品。转化后物品均是单位体积。构造拟阵 M=(E,I)\mathcal{M}=(E,\mathcal{I}) ：

  • EE 是所有物品的集合
  • I={x∣x⊆E,∣x∣≤Max}\mathcal{I}=\{x|x\subseteq E,|x|\leq \text{Max}\}

可以自证 M\mathcal{M} 有上述四个性质。

生成树问题

对于无向图 G=(V,E)G=(V,E) ，我们可以构造 M=(E,I)\mathcal{M}=(E,\mathcal{I}) ：

  • EE 是所有 GG 中的边集 EE 。
  • I={x∣x⊆E,x 组成的图无环}\mathcal{I}=\{x|x\subseteq E,x\text{ 组成的图无环}\}

M\mathcal{M} 可以自证是子集系统。接下来证明 M\mathcal{M} 的交换特性。
取 ∀A∈I\forall A\in I，∀B∈I\forall B\in I，设 ∣A∣<∣B∣|A|<|B| 。我们将 AA 组成的森林称作 GAG_A ，BB 组成的森林称作 GBG_B 。我们一定可以在 GBG_B 中找到一个连通块，满足其在 GAG_A 中不连通。将该连通块在 GAG_A 中连通即可。所以 M\mathcal{M} 具有交换特性。

这个拟阵也称为无向图的图拟阵。

拟阵与最优化

一旦发现了最优化问题的拟阵结构，该最优化问题就可以贪心解决。这是由拟阵的性质决定的。

我们给 EE 中的每个点 xx 标非负权值 w(x)w(x) ，定义 EE 的子集 UU 的权值为 ∑x∈Uw(x)\sum_{x\in U}w(x) ，现在要求 M\mathcal{M} 中的一个最大权值独立集 AA 。

算法的基本思想是按照权值排序 SS 中的每个元素，然后依次选择。如果在目前的 AA 中加入该元素后依然为独立集，那么就选择该元素，否则就放弃。我们通过带入上述的背包问题和生成树问题可以发现，在不同的拟阵模型中，排序算法是大同小异的，算法的明显差异处在于如何判定 A∪{x}∈IA\cup\{x\}\in \mathcal{I} ，而这里一般也是算法的时间复杂度瓶颈。

考虑证明上述贪心策略：我们只需证明在算法的每一步 AA 都是某个最优解的子集，那么当算法结束时 AA 就为一个最优解，因为 AA 无法再扩展了。
假设此时待选择的元素中最大的是 xx ，目前选择的最大权独立集是 AA ，最终的最优解为 TT 。令 A′=A∪{x}A'=A\cup\{x\} ，我们需要证明 A′A' 必然是某个最优解 T′T' 的子集。首先，令 T′=A′T'=A' 。若 ∣T′∣<∣T∣|T'|<|T| ，我们可以通过交换特性不断地将 TT 中 T′T' 没有的元素加入到 T′T' 内。当 ∣T′∣=∣T∣|T'|=|T| 时，T′=(T∖{y})∪{x}T'=(T\setminus\{y\})\cup\{x\} ，其中 yy 是在本应选择 xx 的那一轮中选择的数。显然 w(y)≤w(x)w(y)\leq w(x) ，所以 T′T' 必然是最优解之一。

可以发现，交换特性在拟阵的最优化中发挥了重要作用。

拟阵交

若有 kk 个拟阵定义在同一个全集 EE 上，我们定义这 k 个拟阵 M1=(E,I1),M2=(E,I2),⋯ ,Mk=(E,I2)\mathcal{M_1}=(E,\mathcal{I_1}),\mathcal{M_2}=(E,\mathcal{I_2}),\cdots ,\mathcal{M_k}=(E,\mathcal{I_2}) 的交为 (E,I1∩I2∩⋯∩lk)(E,\mathcal{I_1}\cap\mathcal{I_2}\cap\cdots\cap\mathcal{l_k}) 。
k−k-拟阵交问题为：给定全集 UU 和 MM 个拟阵和正整数 xx ，问能否找到集合 SS ，满足 SS 是拟阵交，且 ∣S∣≥k|S|\ge k 。
当 k≥3k\ge 3 时 k−k-拟阵交问题是 NP-hard\text{NP-hard} （可以规约到哈密顿路径上面去）。当 k=2k=2 时我们有多项式做法，这也是竞赛中最常出现的拟阵交形式。我们先来考虑 k=2k=2 时的拟阵交的算法。
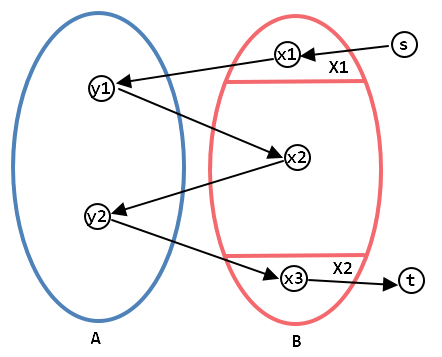
如下图是一个交换系统 GM1,M2(A)G_{\mathcal{M_1},\mathcal{M_2}}(A) ，我们的算法过程在这个交换系统中进行。交换系统 GM1,M2(A)G_{\mathcal{M_1},\mathcal{M_2}}(A) 由两部分点集组成，一部分是当前答案集合 AA ，另一部分是 AA 的补集 B=E∖AB=E\setminus A 。对于边集，如果有从 y∈Ay\in A 连向 x∈Bx\in B 的边，必须满足 (A∖{y})∪{x}∈I1(A\setminus\{y\})\cup \{x\}\in \mathcal{I_1} ；如果有从 x∈Bx\in B 连向 y∈Ay\in A 的边，必须满足 (A∖{y}∪{x})∈I2(A\setminus\{y\}\cup\{x\})\in \mathcal{I_2} 。定义要记清楚。

有了交换系统的概念，我们给出当 k=2k=2 时拟阵交的算法：

  • A=∅A=\emptyset
  • 循环
    • 构造交换图 GM1,M2(A)G_{\mathcal{M_1},\mathcal{M_2}}(A)
    • X1={x∉A∣A∪{x}∈I1}X_1= \{x\notin A|A\cup \{x\}\in \mathcal{I_1}\}
    • X2={x∉A∣A∪{x}∈I2}X_2= \{x\notin A|A\cup \{x\}\in \mathcal{I_2}\}
    • 计算在 GM1,M2(A)G_{\mathcal{M_1},\mathcal{M_2}}(A) 上从点集 X1X_1 到点集 X2X_2 的最短路 PP
    • I=IΔPI=I\Delta P，即将 PP 中属于 AA 的点从 AA 中删去，不属于 AA 的点加入 AA 中 。
  • 当 PP 不存在时，算法结束。
    证明上述算法的正确性要用到最大最小定理以及秩函数的性质。

实际问题中出现的大多是最大带权拟阵交。即给定权值函数 ww ，求

max⁡A∈I1∩I2 ∑x∈Aw(x)\max_{A\in \mathcal{I_1}\cap\mathcal{I_2}}\ \sum_{x\in A}w(x)

我们只需要在交换系统中加入点权

f(x)={−w(x)        x∈Aw(x)        x∈E∖Af(x)=\begin{cases}-w(x)\ \ \ \ \ \ \ \ x\in A\\w(x)\ \ \ \ \ \ \ \ x\in E\setminus A\end{cases}

并将求拟阵交的过程中找最短路的过程改为找以点权和最长为第一关键字的前提下路径长度最长的路径。可以证明上述算法中不存在负环。
证明上述算法的正确性需要用到拓展的最大最小定理。

例题

T1 colorful graph

Description

给定一张 nn 个点 mm 条无向带权边的图，每条边上有颜色 cic_i ，要求在图上保留一个边集，满足

  • 保留的边集使得图连通。
  • 每一种颜色都有至少一条边保留。

求满足条件的情况下边集权值之和的最小值。
n,m≤200,ci≤mn,m\leq 200,c_i\leq m

Solution

拟阵交的题目通常都是：最大权；两个限制条件均要满足。
保留的边集的权值和最小，我们转化为删去的边集的权值和最大。
解题关键是构造拟阵，可以想到应该是两个限制条件每个都构造一个。
对于连通性可以构造拟阵 M1(E,I1)\mathcal{M_1}(E,\mathcal{I_1}) ，其中 EE 为边集，I1={x⊆E∣删去 x 后原图连通}\mathcal{I_1}=\{x\subseteq E|\text{删去 } x \text{ 后原图连通}\} 。传递性很显然，交换性也不难：如果 A∈I1A\in \mathcal{I_1} ，那么意味着原图有一个生成树与 AA 中的边集无交集；如果 B∈I1,∣B∣<∣A∣B\in \mathcal{I_1},|B|<|A| ，我们一定可以找到 AA 中一条 BB 没有的边将其加入 BB 中，且仍然满足拟阵性质。
假设第 ii 种颜色的边总共有 did_i 条，那么对于颜色我们可以构造拟阵 M2(E,I2)\mathcal{M_2}(E,\mathcal{I_2}) ，其中 EE 为边集，I2={x⊆E∣x 中每种颜色的边数至多di−1}\mathcal{I_2}=\{x\subseteq E|x\text{ 中每种颜色的边数至多} d_i-1\} 。传递性和交换性都比较显然。
构造完拟阵后就成了最大带权拟阵交的模板题。

『保留的集合满足某性质』的常用 trick 就是通过『删去某边集后满足某性质』的角度来构造拟阵。因为这样可以确保传递性，也往往容易保证交换性。

Code

const int N=2e2+5,M=2e2+5;
using namespace std;
int n,m,s,t,f[N];
vector<int>G[N];
int inq[N],pre[N],dep[N];
long long now,dis[N],val[N];
vector<long long>ans;
int Find(int x){return x==f[x]?x:f[x]=Find(f[x]);}
vector<int>tmp;
struct edge{
	int u,v,w,c,bel;
	edge(int u=0,int v=0,int w=0,int c=0,int bel=0):
		u(u),v(v),w(w),c(c),bel(bel) {}
}e[M]; 
void Prework(){
	for(int i=1;i<=t;++i) G[i].clear();
	for(int i=1;i<=m;++i){
		if(e[i].bel) continue;
		for(int j=1;j<=n;++j) f[j]=j;
		for(int j=1;j<=m;++j)
			if(!e[j].bel&&i!=j) f[Find(e[j].u)]=Find(e[j].v);
		if(Find(e[i].u)==Find(e[i].v))
			G[s].push_back(i);
		else
			for(int j=1;j<=m;++j)
				if(e[j].bel&&f[Find(e[j].u)]!=Find(e[j].v))
					G[j].push_back(i);
		tmp.clear();bool flag=0;
		for(int j=1;j<=m;++j)
			if(e[j].c==e[i].c&&i!=j)
				if(e[j].bel) tmp.push_back(j);
				else flag=1;
		if(flag) G[i].push_back(t);
		else 
			for(auto j:tmp) G[i].push_back(j);
	}
	for(int i=1;i<=m;++i) val[i]=e[i].bel?-e[i].w:e[i].w;
}
bool update(){
	for(int i=1;i<=t;++i)
		dis[i]=-oo,pre[i]=0,inq[i]=0,dep[i]=m+10;
	queue<int>q;q.push(s);dis[s]=0;inq[s]=1;
	while (!q.empty()){
		int x=q.front();q.pop();
		for(auto u:G[x]){
			if(dis[u]<dis[x]+val[u]||(dis[u]==dis[x]+val[u]&&dep[u]>dep[x]+1)){
				dis[u]=dis[x]+val[u];
				pre[u]=x;
				if(!inq[u]) q.push(u),inq[u]=1;
			}
		}
		inq[x]=0;
	}
	if(dis[t]==-oo) return false;
	now+=dis[t];ans.push_back(now);
	int x=pre[t];
	while(x^s) e[x].bel^=1,x=pre[x];
	return true;
}
int main(){

	ios::sync_with_stdio(0);
	
	cin>>n>>m;s=m+1,t=m+2;
	long long sum=0;
	for(int i=1,u,v,w,c;i<=m;++i){
		cin>>u>>v>>w>>c;
		e[i]=edge(u,v,w,c);
		sum+=w;
	}
	while(Prework(),update()) ;
	long long Max=0;
	for(auto d:ans) 
		Max=max(d,Max);
	cout<<sum-Max<<endl; 
	return 0;
}

T2 rainbow graph

Description

nn 个点 mm 条边的无向图，每条边有三种颜色（RGB），边有边权。要求选择边集 S⊆ES\subseteq E ，满足：

  • ∣S∣=k|S|=k 。
  • 仅保留 SS 中边时，颜色为 RG 的边和颜色为 GB 边分别可以使图连通。

n,m≤100n,m\leq 100 。

Solution

依旧是考虑删边。考虑到拟阵交中边是一条一条删的，所以我们不必对第一个要求设拟阵。强制 m−km-k 次更新即可。
对于第二个要求，实际上这又是两个限制。我们分别构造出拟阵即可。

参考文献

刘雨辰《对拟阵的初步研究》
杨乾澜《浅谈拟阵的一些拓展及其应用》

# 拟阵 # 学习笔记
dijkstra 算法求费用流 上一篇
DP 杂题泛做 下一篇
0%