[JSOI2015] 骗我呢

Description

Solution

首先观察一下题面：它的值域不大。
（值域范围真的是非非非常重要！没开到 $10^9$ 都留个心眼）

值域不大 + 严格单调 = 值域中只能不用若干个数。
也就是说每一排只能放弃值域中的某一个，并且放弃了某个数后这一排就确定了。

我们把第 $i$ 行放弃的数称为 $a_i$ 。所以 $|a| = n$ ，并且 $\{a\}$ 的方案与填数方案一一对应。
剩余的那个限制 $x_{i,j} < x_{i-1,j+1}$ 恰好也可以体现在 $\{a\}$ 上，表现为： $a_i\ge a_{i-1}-1$ 。这个性质画画图不难发现，但是非常重要——将题目要求的限制统一在一个模型中了。

那么现在任意合法的 $\{a\}$ 对应了一个解。转化为了求 $\{a\}$ 的方案数。
设 f[i][j] 表示第 $i$ 个数选 $j$ 的方案数。则

f_{i,j}=\sum_{k=0}^{j+1}f_{i-1,k}

事实上这样的式子通常可以简化转移。因为 $f_{i,j}$ 大部分的值在 $f_{i,j-1}$ 已经算过了。

f_{i,j}=f_{i,j-1}+f_{i-1,j+1}

好的，这个式子就是题解的重点了。

首先画图，这个式子的转移形式是这个样子的：

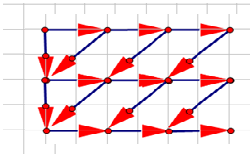
这个转移并不好看。但是我们发现如果把第 $i$ 行右移 $i-1$ 个单位就会很「正」。
为了方便最左侧的点转移，我们新建一个虚拟节点：

此时，最后一行的第 $i$ 个数仅代表了 $a_{n}=i+1$ 时的方案数。为了方便统计答案，我们再加一行，那么第 $n+1$ 行的第 $m+2$ 个数就表示了所有的方案数。
我们将这个图转化到坐标系上（左上角视为 $(0,0)$ ，右下角视为 $(n+m+1,n)$ ），那么每一个转移方案都对应了一条从 $(0,0)$ 到 $(n+m+1,n)$ 的路径。

但是并不是每一条路径都对应了一个合法方案。
因为移动过的关系，所以在任意时刻，都应该有 $y> x-1$ 和 $y< x + m +2$ 。
对应到坐标系上，也就是合法路径任意时刻必须夹在两条平行线之间。

事实上，类比卡特兰数在坐标系中的组合意义可以发现

对于求解从 $(0,0)$ 到 $(a,b)$ ，且任意时刻必须在 $y=x+c$ 上方的路径条数问题，我们可以在当路径碰到 $y=x+c$ 时，将穿过后的路径按照直线 $y=x+c$ 翻折。于是每一条不合法的路径都对应了一条从 $(0,0)$ 到 $(b-c,a+c)$ 的路径。

我们容斥一下，答案即为总方案减去（第一次穿过下边界的方案）减去（第一次穿过上边界的方案）。
其中上边界为直线 $y = x+m+2$ ，下边界为 $y=x-1$ 。

由上面的发现可得：每一条第一次碰到下边界然后到达 $(a,b)$ 的路径一定是一条第一次碰到下边界然后到达 $(b+1,a-1)$ 的路径。碰到上边界同理，就是转化为第一次碰到上边界然后到达 $(b-(m+2),a+(m+2))$ 的方案数。

光从定义上看似乎并没有简化？其实不然。因为对于「第一次碰到下边界然后到达 $(a,b)$ 的路径」我们相当于有两个限制要求：第一次、碰到下边界；而对于「第一次碰到下边界然后到达 $(b+1,a-1)$ 的路径」，事实上只有一个限制要求：第一次。因为我们必然会碰到下边界。上边界同理。

设 $f(x,y)$ 表示从 $(0,0)$ 到 $(x,y)$ ，第一次碰到下边界的方案数。此处有 $y<x-1$ 。
设 $g(x,y)$ 表示从 $(0,0)$ 到 $(x,y)$ ，第一次碰到上边界的方案数。此处有 $y>x+m+2$ 。

由于定义域的限制，我们只需要考虑「第一次」这个要求。容斥可以得到

f(x,y)=\binom{x+y}{x}-g(y-(m+2),x+(m+2))\\ g(x,y)=\binom{x+y}{x}-f(y+1,x-1)

两个函数至多递归 $n+m$ 次，于是我们顺利做完了题目。

Code

const int N = 3e6 + 2333, mod = 1e9 + 7;
using namespace std;
int n, m;
int inv[N], fac[N], invf[N];
inline int binom(int n, int m){
    if(n < 0 or m < 0 or n - m < 0) return 0;
    return 1ll * fac[n] * invf[m] % mod * invf[n - m] % mod;
}
void Prework(int n){
    fac[0] = inv[0] = invf[0] = fac[1] = inv[1] = invf[1] = 1;
    for(int i = 2; i <= n; ++i)
        fac[i] = 1ll * fac[i - 1] * i % mod,
        inv[i] = 1ll * (mod - mod / i) * inv[mod % i] % mod,
        invf[i] = 1ll * invf[i - 1] * inv[i] % mod;
}
int g(int x, int y);
int f(int x, int y){ // beyond dn-border first
    if(x < 0 or y < 0) return 0;
    return (binom(x + y, x) + mod - g(y - (m + 2), x + (m + 2))) % mod;
}
int g(int x, int y){ // beyond up-border first
    if(x < 0 or y < 0) return 0;
    return (binom(x + y, x) + mod - f(y + 1, x - 1)) % mod;
}
int main(){

    Prework(3e6 + 23);
    r(n, m);
    int ans = binom(n + n + m + 1, n);
    (ans += mod - f(n + m + 2, n - 1)) %= mod;
    (ans += mod - g(n - 1, n + m + 2)) %= mod;
    ans = (ans % mod + mod) % mod;
    w(ans); 
    return 0;
}

Reference

图片来自这篇博客

Description

Solution

Code

Reference

感谢您的支持，我会继续努力的!