CF932G Palindrome Partition

Description

给定一个串，把串分成偶数段，假设为 $s_1,s_2,\cdots,s_k$ ，要求满足 $s_1=s_k,s_2=s_{k-1},\cdots$ ，求方案数。
$n\leq 10^5$

Solution

标题透露算法系列
首先这道题有个神仙性质。

设 t=s[1]s[n]s[2]s[n-1]... ，那么 t 串的一个偶回文划分对应着 s 串的一个题目要求的划分。

没发现性质是真的不好想...但是知道了以后可以通过归纳来证明。

whatever，现在问题转化为求一个串的偶回文划分方案数。
考虑暴力做法。设 f[p] 表示以 p 结尾的前缀的偶回文划分方案数。那么我们构建出 PAM ，然后在 fail 树上跳，判断是否是偶回文串并暴力更新。这样的复杂度是 $\mathcal{O}(n^2)$ 的。
考虑回文树上 fail 的性质

回文串的最大回文后缀是其 border 。
当最大回文后缀长度不小于原串长度的一半时，最大回文后缀在原串中仅出现两次，一次作为原串前缀，一次作为原串后缀。

根据上述性质，我们把 DP 的过程绘制出来，看看如何优化。

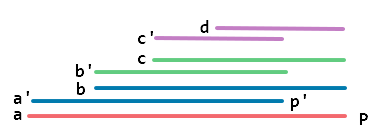
如图，上面的字符串是下面的字符串长度不小于一半的最大回文后缀。
如果暴力更新，此时 f[p] 应该是 f[a]+f[b]+f[c]+f[d] 。
可以观察到，f[p] 的大部分值其实在 f[p']=f[a']+f[b']+f[c'] 处计算过了。
当然，在 f[p'] 处我们不一定计算了其值。所以我们另设 g[p] ，表示在 PAM 上以 p 为末项的等差数列的 $\sum f$ ，就可以快速更新 f[p] 了。

还有一个问题：万一 f[a] 更新了 f[p] ，但是 t[a:p] 是奇回文串怎么办？没关系，考虑到原数组中只有偶数的位置应该有 f 值，我们可以强制不转移到奇数位置。当 p 是偶数位置时，能更新到 p 的位置也只能是偶数位置，其中的字符串自然就是偶回文串了。

不在同一个等差数列里的至多只有 $\log_2n$ 组，所以复杂度为 $\mathcal{O}(n\log_2{n})$ 。

Code

const int N=1e6+5,mod=1e9+7;
using namespace std;
char s[N],t[N];
namespace PAM{
    int dfn,las,top,tot;
    int dif[N],bot[N],pos[N];
    int f[N],g[N];
    struct node{
        int len,fail,c[26];
    }a[N];
    int getfail(int x){
        while(s[top]!=s[top-a[x].len-1])
            x=a[x].fail;
        return x;
    }
    void extend(int k){
        ++top;
        int cur=getfail(las);
        if(!a[cur].c[k]){
            int now=++tot;
            a[now].len=a[cur].len+2;
            a[now].fail=a[getfail(a[cur].fail)].c[k];
            dif[now]=a[now].len-a[a[now].fail].len;
            bot[now]=dif[now]==dif[a[now].fail]?bot[a[now].fail]:now;
            a[cur].c[k]=now;
        }
        las=a[cur].c[k];
    }
    void build(char *s){
        int len=strlen(s+1);
        las=tot=1;top=0;
        a[0].len=0,a[1].len=-1;
        a[0].fail=a[1].fail=1;
        for(int i=1;i<=len;++i)
            extend(s[i]-'a'),pos[i]=las;
    }
    void solve(int n){
        f[0]=1;
        for(int i=1;i<=n;++i)
        for(int j=pos[i];j;j=a[bot[j]].fail){
            int t=bot[j];
            if(t!=j) g[j]=g[a[j].fail];
            else g[j]=0;
            if(a[t].len) 
                g[j]=(g[j]+f[i-a[t].len])%mod;
            if(i%2==0) 
                f[i]=(f[i]+g[j])%mod;
        }
        printf("%d\n",f[n]);
    }
}
int main(){

    scanf("%s",t+1);
    int len=strlen(t+1);
    for(int i=1;i<=len;++i)
        s[i]=i%2==0?t[len-i/2+1]:t[i+1>>1];
    PAM::build(s);
    PAM::solve(len);
    return 0;
}